set.seed(123)
data<-read.csv2("C:/Users/guill/OneDrive/Documents/Charles_University/Multivariate analysis/Europe.csv",sep=";",header = TRUE,row.names = 1,dec=",")
library(FactoMineR)

require(foreign)
## Le chargement a nécessité le package : foreign
require(nnet)
## Le chargement a nécessité le package : nnet
require(ggplot2)
## Le chargement a nécessité le package : ggplot2
require(reshape2)
## Le chargement a nécessité le package : reshape2

Create 3 groups for a lda.

Because I don’t have a group in my database

data_scale <- scale(data)
resKmeans <- kmeans(data_scale, 3, nstart = 50)
data$class<-resKmeans$cluster
library(MASS)
lda1 <- lda(class ~ ., data = data)
lda1cv <- lda(class ~ ., data = data,CV=T)

pred <- predict(lda1)
ldahist(data = pred$x[,1], g=data$class)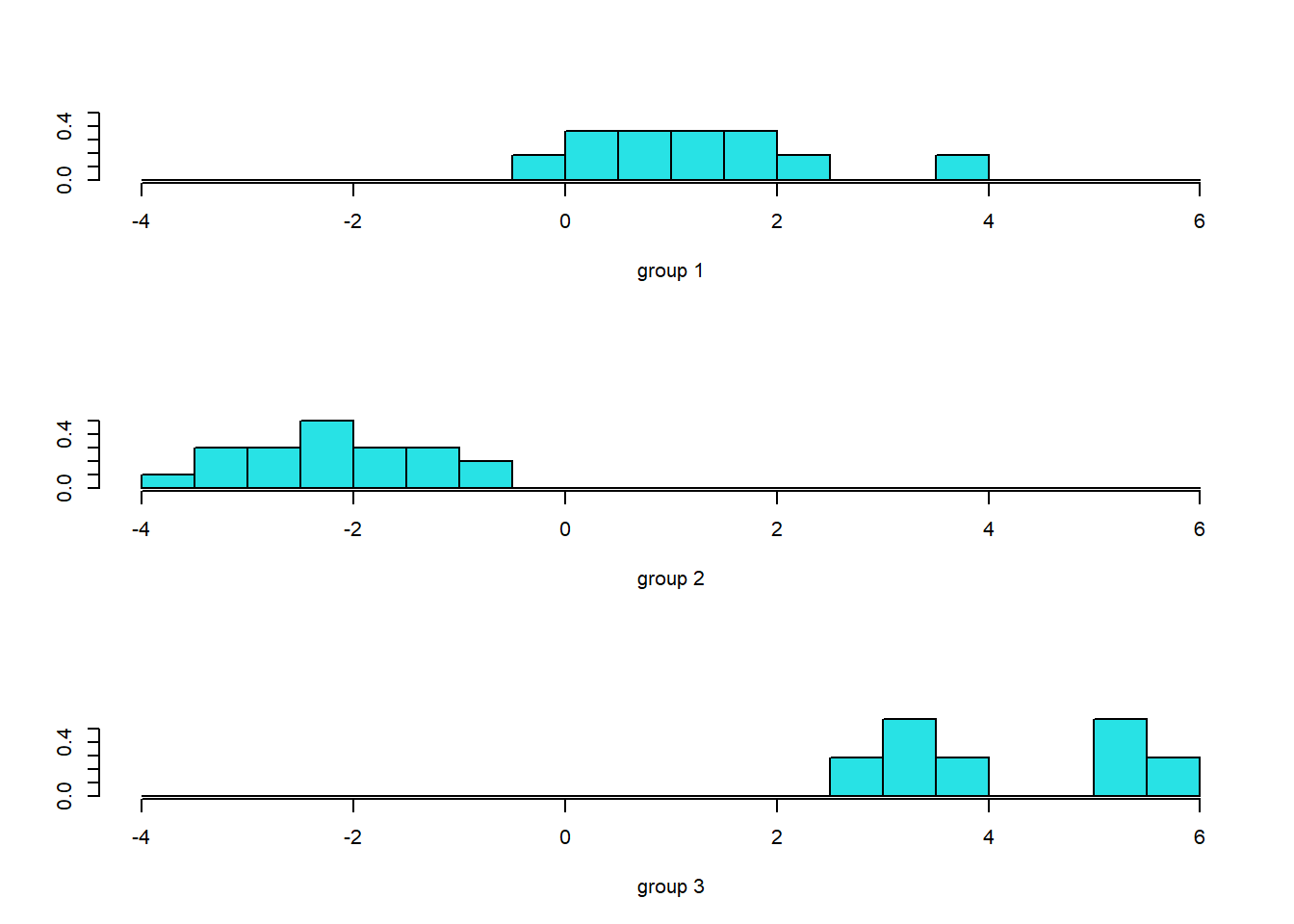

library("klaR")
tData <- cbind(as.matrix(data[,1:9]) %*% lda1$scaling, data$class)

m1 <- apply(tData[tData[,3] == 1, 1:2], 2, mean)
m2 <- apply(tData[tData[,3] == 2, 1:2], 2, mean)
m3 <- apply(tData[tData[,3] == 3, 1:2], 2, mean)
plot(tData[,2] ~ tData[,1], pch = 22, bg = c("red", "yellow", "green")[unclass(as.factor(data$class))], xlab = "First LDA direction", ylab = "Second LDA direction")
points(m1[1], m1[2], cex = 2, pch = 21, bg = "red")
points(m2[1], m2[2], cex = 2, pch = 21, bg = "yellow")
points(m3[1], m3[2], cex = 2, pch = 21, bg = "green")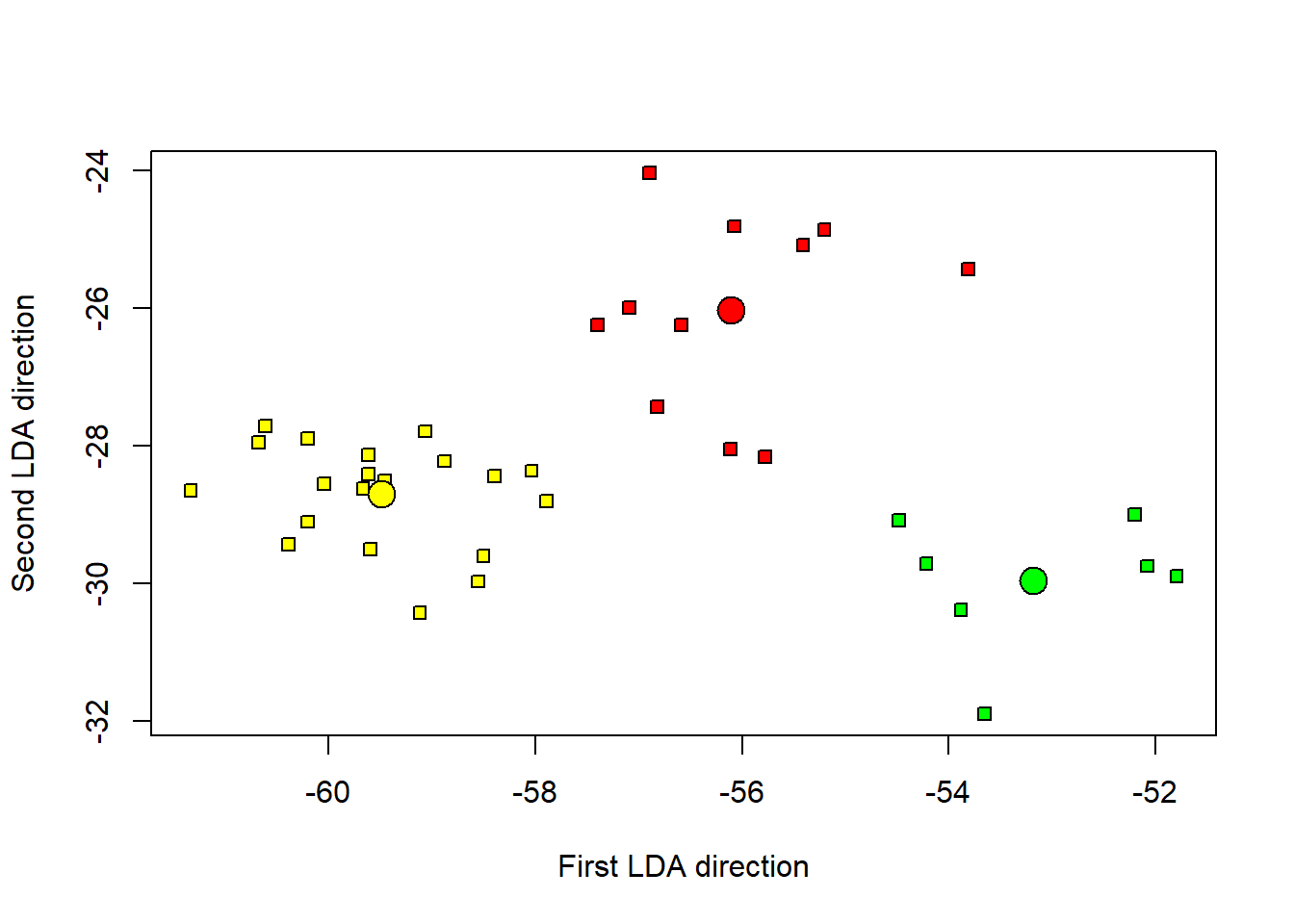

The three groups are well distinguished

test<-multinom(as.factor(class)~.,data=data)
## # weights:  33 (20 variable)
## initial  value 41.747267 
## iter  10 value 15.495431
## iter  20 value 0.758328
## iter  30 value 0.001463
## final  value 0.000062 
## converged
z<-summary(test)$coefficients/summary(test)$standard.errors
(1 - pnorm(abs(z), 0, 1)) * 2
##   (Intercept) Fertility GDP.per.capita Life.expectancy Meat.consumption
## 2           0         0      0.9816486       0.6838418        0.9957911
## 3           0         0      0.9530796       0.0000000        0.0000000
##   Median.age Population.growth Sex.ratio Suicide.rate Urbanization.rate
## 2          0                 0         0            0         0.9721808
## 3          0                 0         0            0         0.0000000
lda2 <- lda(class ~Population.growth , data = data)
lda2cv <- lda(class ~Population.growth , data = data,CV = T)
lda_scores <- as.numeric(lda2$scaling) * data$Population.growth
par(mfrow = c(1,2))
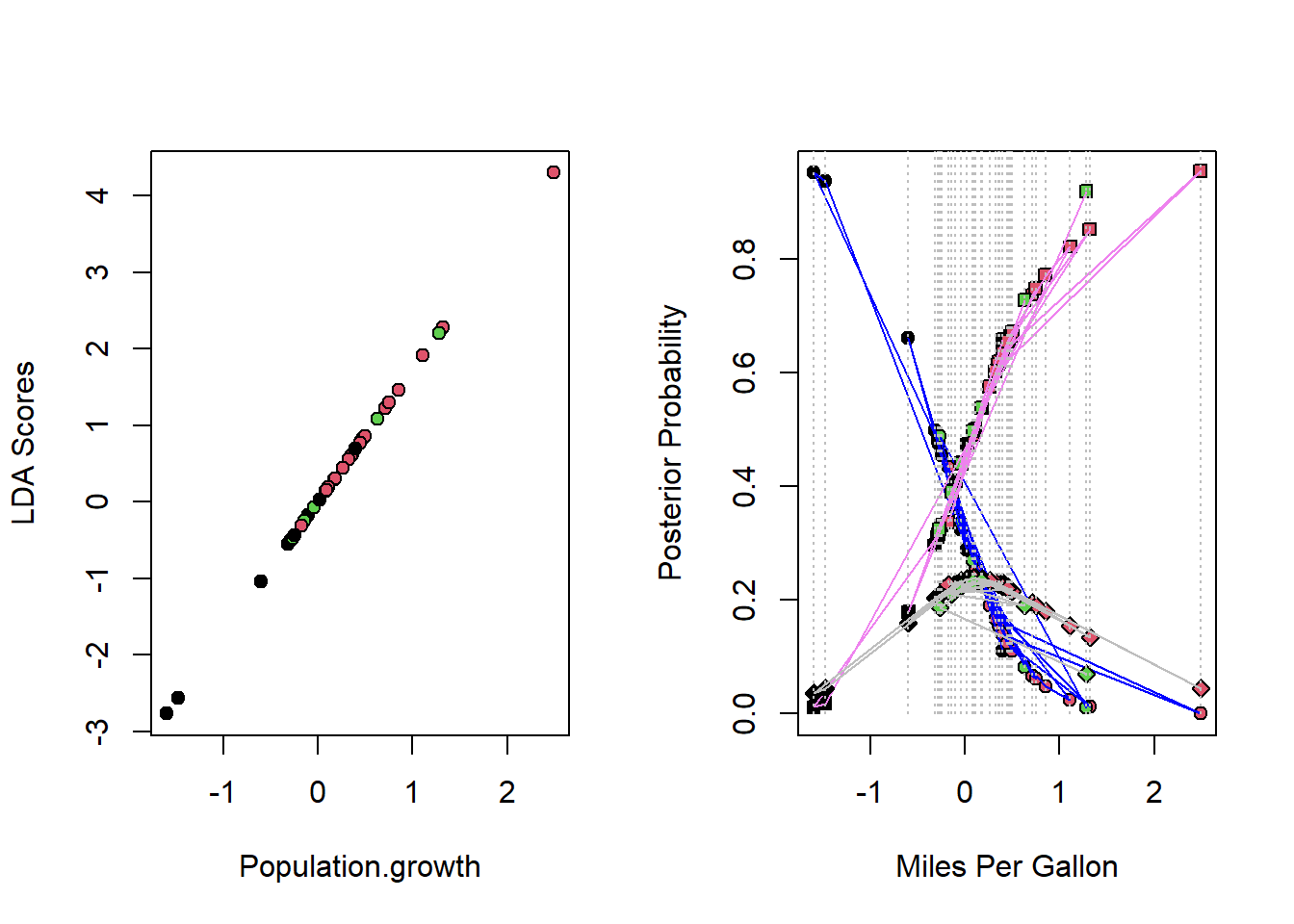
plot(lda_scores ~ data$Population.growth, pch = 21, bg = data$class, ylab ="LDA Scores", xlab = "Population.growth")

lda2cv <- cbind(lda2cv$posterior, data$Population.growth, data$class)
lda2cv <- lda2cv[order(data$class), ]

plot(lda2cv[,1] ~ lda2cv[,4], pch = 21, bg = lda2cv[,5], ylab = "Posterior Probability", xlab = "Miles Per Gallon")
lines(lda2cv[,1] ~ lda2cv[,4], col = "blue")
points(lda2cv[,2] ~ lda2cv[,4], pch = 22, bg = lda2cv[,5])
lines(lda2cv[,2] ~ lda2cv[,4], col = "violet")
points(lda2cv[,3] ~ lda2cv[,4], pch = 23, bg = lda2cv[,5])
lines(lda2cv[,3] ~ lda2cv[,4], col = "gray")

for (i in 1:nrow(lda2cv)){
  lines(rep(lda2cv[i,4], 2), c(0,1), col = "gray", lty = 3)
}

data2<-data
data_scale2 <- scale(data2)
resKmeans2 <- kmeans(data_scale2, 2, nstart = 50)
data2$class<-resKmeans2$cluster
library("FactoMineR")
library("factoextra")
## Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa

Create PCA

res<-PCA(data2,quali.sup=10,graph = F)
data3<-data.frame(cbind(res$ind$coord[,1:2],data2$class))
colnames(data3)[3]<-"class"
fviz_pca_var(res, col.var = "black")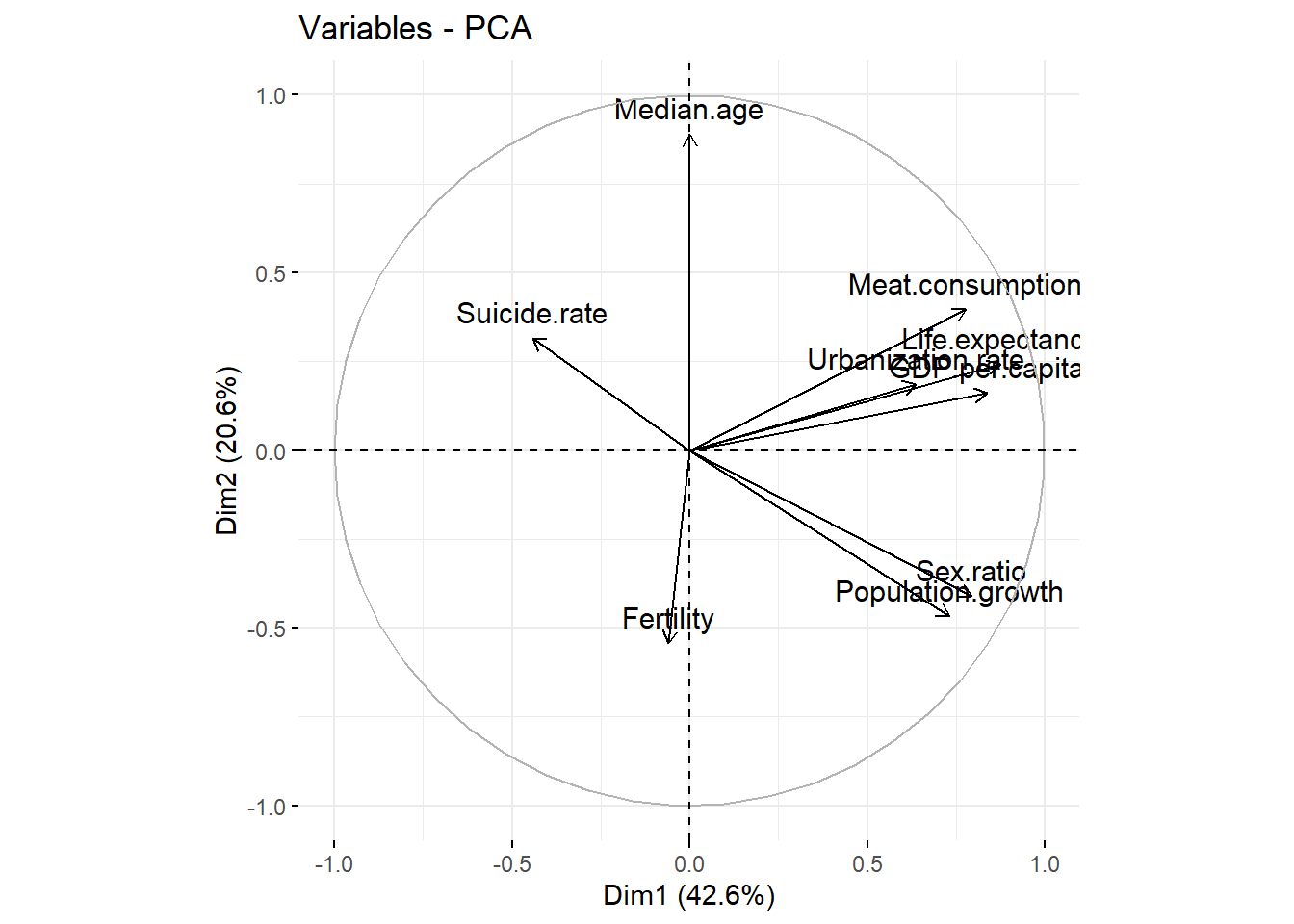

da.gr = data.frame(cbind(seq(-3.5,5,len=38),seq(-5,3,len=38)))
names(da.gr) = c("Dim1","Dim2")
par(mfrow=c(2,2))
cols <- c("red", "blue")
mowe.ii = unique(da.gr$Dim1)
mowe.ll = unique(da.gr$Dim2)
d.nn <- glm(factor(class)~Dim.1+Dim.2,family=binomial,data=data3)
## Warning: glm.fit: l'algorithme n'a pas convergé
## Warning: glm.fit: des probabilités ont été ajustées numériquement à 0 ou 1
summary(d.nn)
## 
## Call:
## glm(formula = factor(class) ~ Dim.1 + Dim.2, family = binomial, 
##     data = data3)
## 
## Deviance Residuals: 
##        Min          1Q      Median          3Q         Max  
## -2.846e-05  -2.100e-08  -2.100e-08   2.100e-08   3.389e-05  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept)   -15.20   33244.67   0.000    1.000
## Dim.1         -52.47   42088.60  -0.001    0.999
## Dim.2          17.05   30967.49   0.001    1.000
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 5.2257e+01  on 37  degrees of freedom
## Residual deviance: 2.5728e-09  on 35  degrees of freedom
## AIC: 6
## 
## Number of Fisher Scoring iterations: 25